人工智能基础
人工智能基础
核心思想
基于已知数据构造概率模型,反过来再运用概率模型对未知数据进行预测与分析。
频率学派与统计学习
频率学派所说的概率表示的是 事件发生频率的极限值,在无限次独立重复实验下才准确。
频率统计理论的核心在于认定待估计的参数是固定不变的常量(比如硬币出现正面的概率),讨论参数的概率分布是没有意义的;而用来估计参数的数据是随机的变量(比如某次实验正面还是反面),每个数据都是参数支配下一次独立重复试验的结果。由于参数本身是确定的,那频率的波动就并非来源于参数本身的不确定性,而是由有限次观察造成的干扰而导致。
有限次的实验得到的数据是关于参数的不完全信息,所以从样本估计整体必然产生误差。
极大似然估计:在参数固定的前提下,使数据出现的条件概率最大化。
统计机器学习
参数确定,数据随机
通过对给定的指标优化(比如极大似然函数),估计模型中参数的取值,和参数有关的信息全来自数据。受噪声的影响,观测数据并不是未知参数的准确反映,损失函数定义了模型性能的度量方式,其期望称为风险,风险最小化是参数估计的准则。
贝叶斯学派
概率表示的是客观上 事件的可信程度。
梯度下降公式的推导
目标是最小化一个可微函数
函数
函数
保留一阶泰勒展开,得到
其中
表示移动方向与梯度方向相反,自然选择
其中
以回归模型为例,用
其代价函数为
偏导数计算如下
则更新规则为
这种方法需要再执行单次更新前扫描整个训练集,被称为 批量梯度下降。
线性回归
设模型的预测值为
单个样本
其中
若有
于是,最大化似然函数
对于单变量的线性回归,
对于多变量的线性回归,
定义损失函数为
令
泛化和正则
泛化
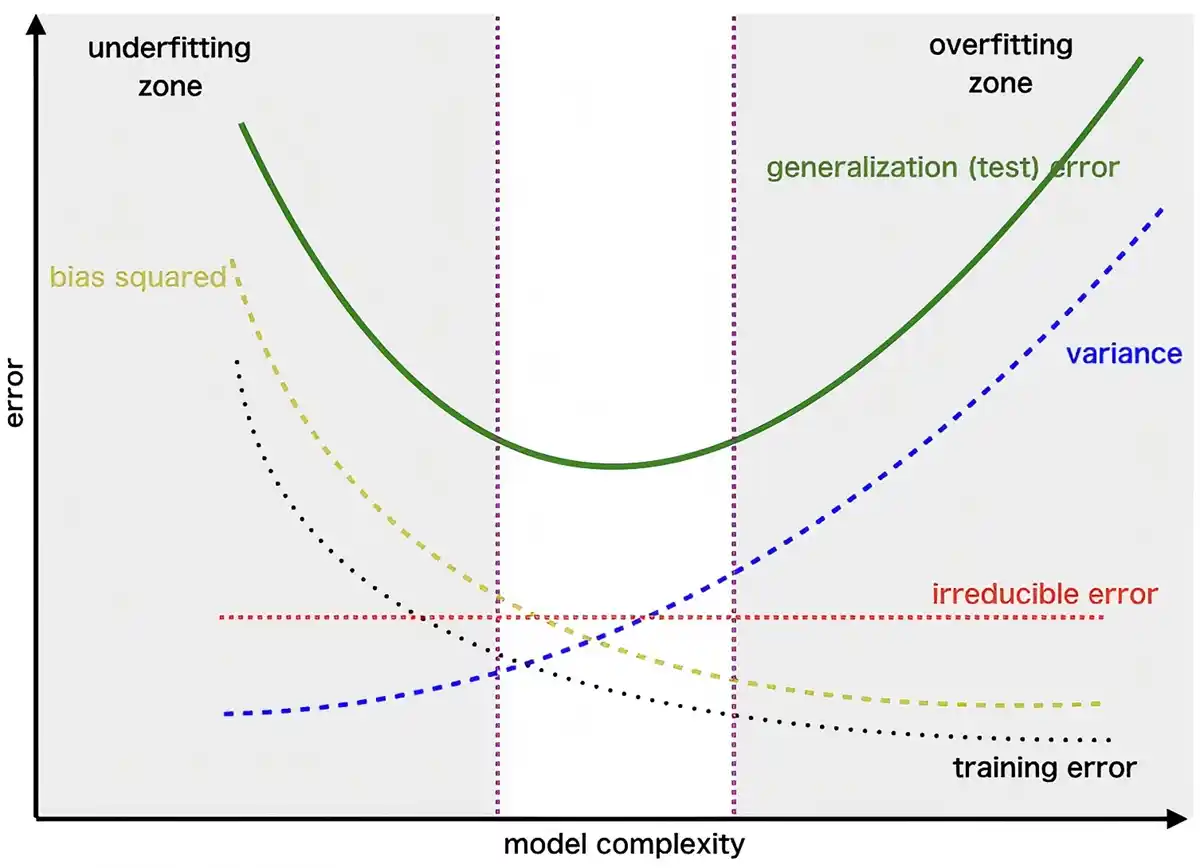
偏差-方差均衡
训练集输入
将模型的 偏差(bias) 定义为即使拟合到无限大的训练数据集,曾存在的测试误差。在这种情况下,表现为欠拟合。
训练集中的虚假信息大部分是由于观测噪声
引起的,拟合这些虚假信息会导致模型具有较大的测试误差,将其定义为模型的方差。 通常,偏差和方差之间存在权衡。如果模型过于简单且参数很少,那么它可能具有较大的偏差(但方差较小),并且通常会遭受欠拟合;如果它过于复杂且参数很多,那么它可能遭受较大的方差(但偏差较小),因此会过拟合。
- 对于回归问题的数学分解——偏差-方差权衡
抽取一个训练集
下面将
抽取无限多个数据集作为训练集,对他们在
如前所述,偏差本质上是由于模型族本身无法很好地近似
传统偏差-方差权衡的扩展
- 模型层面
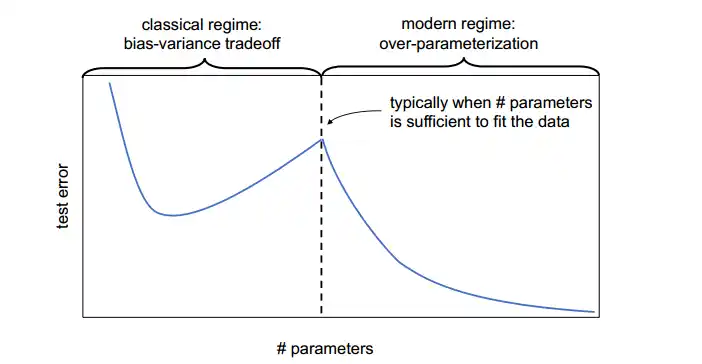
当模型复杂度逐渐增大时,训练误差持续下降,而测试误差先下降后上升,形成传统的 U 形曲线。当模型继续变大到 恰好能将训练数据完全拟合 之上时,测试误差再次下降,形成第二次下降,于是整体呈现 双下降 形状。
- 样本层面
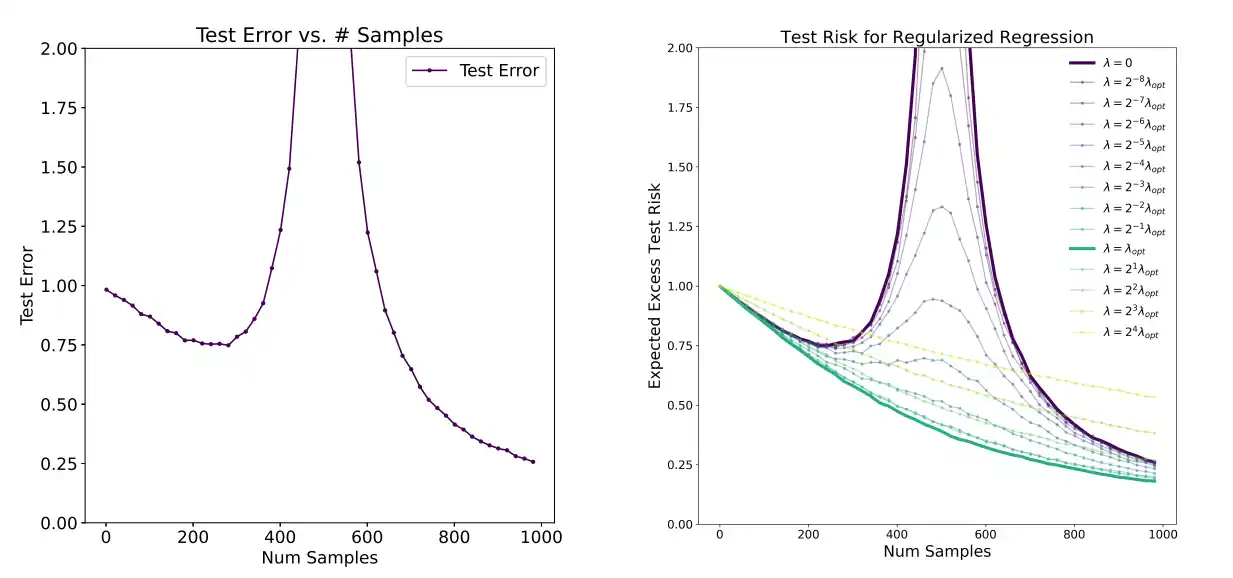
随着样本数量的增加,测试误差并非单调递减。而是测试误差先下降,然后在样本数量与参数数量接近时增加并达到峰值,然后再次下降。
因此,多数的训练算法在样本数量接近参数数量时,没有达到最优结果。例如在使用梯度下降优化器时,算法可能找到拟合数据的任意解,导致泛化误差增大。
缓解策略包括:调整正则化参数;避免以参数数量作为复杂度度量;
正则
在训练损失函数中添加一个附加项
正则项
目标是既能以很小的损失拟合数据,又能有较小的模型复杂度。
以
交叉验证
假设有一些有限的模型集合
通过 留出交叉验证 选择模型,给定一个训练集
- 随机将
- 仅在
- 选择在留出交叉验证集上误差
通常,交叉验证集占数据量的
- 随机将
- 对于每个模型,对于
- 模型
- 选择泛化误差最小的模型,并在整个训练集
贝叶斯与正则化
前文的参数拟合使用的是最大似然估计,将
另一种方法是贝叶斯方法,将参数
其中
当给定一个新的测试样本
计算后验分布需要对
积分,无法得到闭式解。实际使用时,采用近似方法(单点估计)